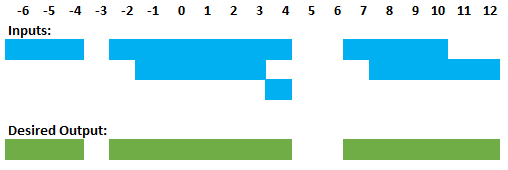Here’s the problem: you have a table with overlapping intervals and want to “pack” the intervals to remove the overlaps, thereby making each interval continuous.
That’s OK if you didn’t understand that. I didn’t either until just recently. Packing intervals is not an uncommon problem in the world of relational databases, and there are many ways to solve it.
The purpose of this blog post is to analyze one particular solution. I’ll be focusing not on the mechanics of the solution’s algorithm (although that’s a natural by-product of this analysis), but the intuition and chain of reasoning used to create a solution for a problem like this. I’ve created two SQL Fiddles: one showing the steps to produce the intermediate outputs, and the other showing the complete solution. The code is SQL Server T-SQL, but it’s pretty generic so porting it to a different platform shouldn’t be a major hurdle.
Before we begin, I want to thank my favorite SQL author, Itzik Ben-Gan. I’ve enjoyed reading several of his books and blog posts. He has the enviable skill of writing clearly about the entire length and breadth of SQL. I wish to stress that the solution I present here is his, not mine. It comes primarily from his book “Microsoft SQL Server 2012 High-Performance T-SQL Using Window Functions”, on page 198.
I’d also like to note that I’m not going to address the solution’s performance. Itzik Ben-Gan has a blog post covering the topic of performance of several different solutions in detail, so I won’t repeat any of that here.
Let’s get started!
The table we’re working with has a very simple structure. I didn’t include a primary key, indexes or check constraints because I want the code to be as simple as possible, and – as I just noted – this analysis is not concerned with performance.
CREATE TABLE dbo.Inputs ( range_start INT NOT NULL, range_end INT NOT NULL );
This is the input data. Note the overlaps between the different ranges:
range_start range_end ----------- ----------- -6 -4 -2 4 -1 3 4 4 7 10 8 12
After merging the overlaps, the desired output looks like this:
range_start range_end ----------- ----------- -6 -4 -2 4 7 12
Here’s a graphical depiction of the input and desired output:
So, we’ve got inputs and outputs. Now we have to create an algorithm to transform the inputs into the desired output. But…where to start?
If you’re not comfortable with SQL and the relational model, it may be tempting to use a CURSOR and WHILE loop to create the output. This is almost always a mistake. A relational database was never intended to be treated like a file store, and generally performs poorly when treated as such. Playing to SQL’s strengths by using a mathematical set-oriented approach is the way to go.
Since SQL Server doesn’t have a PACK INTERVAL operator, there’s no single step that takes us from the input to the output. This means we have to develop a multiple-step algorithm. We have a choice of two starting points in developing the algorithm: work forward from the input result set, or backwards from the output result set. Working backwards has an obvious first step, so we’ll start there.
The obvious step is that since we know what the output looks like, we can infer what the SQL statement used to generate it will look like. The range_start column contains minimum values, and the range_end column contains maximum values. So the MIN and MAX functions are probably going to be used. Also, the rows in the output result set appear to be summaries of the input result set’s rows. That implies the GROUP BY clause will be present. The SQL that creates the output will probably look something like this:
SELECT MIN(range_start), MAX(range_end) FROM Ranges GROUP BY some_grouping_value_we_havent_discovered_yet;
From this we can work another step backwards by observing that the Ranges table looks just like the original input table, but with a grouping value:
range_start range_end some_grouping_value_we_havent_discovered_yet ----------- ----------- -------------------------------------------- -6 -4 1 -2 4 2 -1 3 2 4 4 2 7 10 3 8 12 3
We need to create the grouping value. Most of the time a grouping value is either already present in the data, or there’s an obvious way to create one. Alas, neither is the case here, so we’ve got some work to do. Let’s start by investigating nature of the grouping value.
Looking at the data above, we can see that the grouping value has two special properties:
- It remains constant within a range’s overlapping intervals.
- It increments whenever it crosses a gap between the range intervals. Knowing how the
GROUP BYclause works, the grouping value does not have to increment by 1. Instead of 1, 2, and 3, the example grouping values above could just as easily be -42, 27 and 999, and theSELECTstatement would still create the correct output.
Let’s tackle property #1 first. The grouping value is related to the ranges, but in their current state the ranges are difficult to deal with. They consist of values in not one but two columns. The difference between range_start and range_end can be any value between the minimum and the maximum value for that datatype. The example ranges are INTs, so the min and max values are -231 (-2,147,483,648) to 231-1 (2,147,483,647). This means the ranges themselves don’t have any useful pattern that we can use to directly create a grouping value. Given this, it seems like simplifying the range data would a good first step. And here’s where intuition comes into our algorithm design.
Intuition #1: Convert range values into scalars
Each range consists of one or more scalar values, but they’re in two columns, and the individual scalars are kind of “hidden” in that they’re not explicitly present in the data. For example, the range -1 to 3 contains the scalar values -1, 0, 1, 2, and 3. But looking at the input data, 0, 1, and 2 are only implied – they’re not really “there”, are they?
Looking at what’s blocking our progress (ranges split across two columns, and the ranges’ scalar components being hidden), it seems the way forward is to create a new column with all of the ranges’ scalars.
Intuition #2: Using a number table to convert the range values into scalars
Again, one might be tempted to use a CURSOR here, but – as always – that’s going to cause far more pain than pleasure. In the world of SQL, there’s a very neat technique using something called a number table (or, when dealing with dates and times, its cousin the calendar table).
Number and calendar tables are immensely useful in SQL programming. Unfortunately, when trying to solve a thorny SQL problem, there’s no flashing neon sign saying “use a number table here”. Much like creating a mathematical proof, one’s knowledge of SQL, experience, and intuition are all necessary when creating a solution. In this case, simply joining each range with rows from a number table “expands” the ranges into their constituent scalar values. This SQL:
SELECT I.range_start, I.range_end, range_value = N.N FROM dbo.Inputs AS I INNER JOIN Numbers AS N ON N.N BETWEEN I.range_start AND I.range_end;
produces this table:
range_start range_end range_value ----------- ----------- ------------- -6 -4 -6 -6 -4 -5 -6 -4 -4 -2 4 -2 -2 4 -1 -1 3 -1 -2 4 0 -1 3 0 -2 4 1 -1 3 1 -2 4 2 -1 3 2 -2 4 3 -1 3 3 -2 4 4 4 4 4 7 10 7 7 10 8 8 12 8 7 10 9 8 12 9 7 10 10 8 12 10 8 12 11 8 12 12
(The Numbers table is just a single column of integers, ranging from the minimum range_start value to the maximum range_end value.)
Now we’re getting somewhere. Instead of unwieldy pairs of range values, we now have a single column of integers (range_value). Also, the gaps between the overlapping intervals have been preserved. The ranges are now much easier to deal with on a relational basis. Note that this behavior aligns with property #2 of the grouping values, as stated above. Each gap in range_value represents a kind of increment between each range.
(Don’t worry about the duplicate range_start and range_end values. Look back at the final SQL statement (the one with the GROUP BY) that’s going to generate the desired output. It’s calling the MIN and MAX functions, which don’t care about duplicate data. If they don’t care, neither do we.)
We’re almost there. Just one more thing has to fall into place to get a true grouping value, and it requires another intuitive leap.
Intuition #3: Offset
Looking at the desired output above, the some_grouping_value_we_havent_discovered_yet column looks like it could be an offset between the three range groups, doesn’t it? Following this line of thought, maybe we could calculate an offset between range_value (which has gaps), and a new column of similar values that doesn’t have gaps. Simple subtraction would yield a value which can (finally!) be used as a true grouping value.
It so happens that most modern SQL implementations have something called window functions. The four basic functions are ROW_NUMBER, NTILE, RANK, and DENSE_RANK. What we need is a function that produces a sequence of values that has duplicates like range_value, but no gaps. Only DENSE_RANK has those two properties. Here’s what applying DENSE_RANK over range_value looks like:
SELECT I.range_start, I.range_end, range_value = N.N, [dense_rank] = DENSE_RANK() OVER (ORDER BY N.N) FROM dbo.Inputs AS I INNER JOIN Numbers AS N ON N.N BETWEEN I.range_start AND I.range_end; range_start range_end range_value dense_rank ----------- --------- -------------------- -------------------- -6 -4 -6 1 -6 -4 -5 2 -6 -4 -4 3 -2 4 -2 4 -2 4 -1 5 -1 3 -1 5 -2 4 0 6 -1 3 0 6 -2 4 1 7 -1 3 1 7 -2 4 2 8 -1 3 2 8 -2 4 3 9 -1 3 3 9 -2 4 4 10 4 4 4 10 7 10 7 11 7 10 8 12 8 12 8 12 7 10 9 13 8 12 9 13 7 10 10 14 8 12 10 14 8 12 11 15 8 12 12 16
To get a true grouping value, we just perform the subtraction (range_value - dense_rank) and put the result into a table called Groups:
SELECT I.range_start, I.range_end, range_value = N.N, [dense_rank] = DENSE_RANK() OVER (ORDER BY N.N), grouping_value = N.N - DENSE_RANK() OVER (ORDER BY N.N) FROM dbo.Inputs AS I INNER JOIN Numbers AS N ON N.N BETWEEN I.range_start AND I.range_end; range_start range_end range_value dense_rank grouping_value ----------- --------- -------------------- -------------------- -------------------- -6 -4 -6 1 -7 -6 -4 -5 2 -7 -6 -4 -4 3 -7 -2 4 -2 4 -6 -2 4 -1 5 -6 -1 3 -1 5 -6 -2 4 0 6 -6 -1 3 0 6 -6 -2 4 1 7 -6 -1 3 1 7 -6 -2 4 2 8 -6 -1 3 2 8 -6 -2 4 3 9 -6 -1 3 3 9 -6 -2 4 4 10 -6 4 4 4 10 -6 7 10 7 11 -4 7 10 8 12 -4 8 12 8 12 -4 7 10 9 13 -4 8 12 9 13 -4 7 10 10 14 -4 8 12 10 14 -4 8 12 11 15 -4 8 12 12 16 -4
Success!
Now the SQL to create the desired output will work. The statement:
SELECT range_start = MIN(range_start), range_end = MAX(range_end) FROM Groups GROUP BY grouping_value;
produces this output:
range_start range_end ----------- ----------- -6 -4 -2 4 7 12
Takeaways
- Learn SQL and the relational model. They’re really not that bad. Taking the time to pick apart problems like this – in any technology – pays huge dividends in the long run.
- If you’re tempted to use a
CURSOR, please don’t. Both SQL and the relational model are specifically designed for set operations, not file scanning. - On a related note, be wary of ORMs, too. Trying to solve problems like this with an ORM, rather than SQL, will probably fall somewhere between difficult and impossible.
- Beware cargo cult programming, which leads directly to technical debt. Simply copying a solution like this into your code, without a basic understanding of how it works, incurs a high risk of expensive problems later on.